Ch. 6 & Ch. 7: Applications of \(t\)-tests

STAT 218 - Week 6, Lecture 4 Lab 4

What Have We Learned So Far?

A Snapshot

Descriptive Statistics describes and summarizes data.
- Includes understanding
  - distribution shape (skewed, normal, etc.),
  - central tendency (mean, median, mode), and
  - spread (variance, standard deviation, range).
Inferential Statistics makes predictions and draws conclusions about populations based on sample data.
- We saw different types of t-tests:
  - One sample t-test: compares a sample mean to a known or hypothesized population mean.
  - Independent samples t-test: compares means of two independent groups.

Estimation and Hypothesis Testing

We learned that we can estimate the unknown parameters in two ways:

Point estimation: A single value calculated from the sample (e.g., \(\bar{y}\))
Confidence Intervals: A range of values within which the parameter is expected to fall, with a certain degree of confidence.(e.g., 95% CI, 90% CI)

We also learned that we can use hypothesis testing to test for a specific value(s) of the parameter.

e.g., \(H_0: \mu = 76\) cm & \(H_A: \mu \neq 76\) cm (Two-tailed test)
\(H_0: \mu_1 - \mu_2 = 0\) cm \(H_A: \mu_1 > \mu_2\) (One-tailed test)

Hypothesis Testing Steps

Introduction

Important

We can summarize hypothesis testing in five steps:

Construct the Hypotheses of \(H_0\) and \(H_A\)
Determine your \(\alpha\) level
Check the assumptions (We will see this today)
Compute test statistic and find the P-value (Interpreting R Output)
Draw conclusion.

Assumptions - Verification of Conditions

It is always important to check first whether the conditions are reasonable in a given case.
Here is the list of conditions that we should be aware of for \(t\)-tests.

1) Random Sampling: the data can be regarded as coming from independently chosen random sample(s),

2) Independence of Observations: the observations should be independent, and

3) Normal Distribution: Many of the methods depend on the data being from a population that has a normal distribution.

REMEMBER! If sample size is large, then condition (3) is less important (Central Limit Theorem).

Normality Assumption - I

If the only source of information is the data at hand, then normality can be roughly checked.
- Unfortunately, for a small or moderate sample size, this check is fairly rudimentary.
- If the sample is large, then the visual plots (histogram and normal quantile plot) give us good information about the population shape;
  - However, if \(n\) is large, the requirement of normality is less important anyway due to the Central Limit Theorem.
In any case, a rudimentary check is better than none, and every data analysis should begin with inspection of a graph of the data, with special attention to any observations that lie very far from the center of the distribution.

Normality Assumption - II

We check assumptions before conducting any statistical analysis. To check normality assumption, we need to first check sample size.

\(1^{st}\) option - small samples: Check the \(p\)-value of Shapiro Wilk test. It is best used with a sample size less than 50 (Shapiro & Wilk 1965; Uttley,2019).
\(2^{nd}\) option - large samples: Check the visual plots (e.g., histogram, normal quantile plot) if your sample size is more than 50.

Today we will have large samples so we will learn Shapiro-Wilk next week

One Sample \(t\)-test

To-do List Before Start

Download the worksheet and from Canvas (Lab Assignment 4).
Save them to your STAT 218 folder.
Open my slides and the worksheet together. Follow the instructions from the worksheet and get help from my slides if you need it! Call me over if you have any questions

Introduction

In one sample \(t\) tests, data collected from one sample and compares the mean score with a test value.
- Test value can be
1. reported previously in the literature; or
2. found by calculating level of chance.

Introduction - II

To begin with, we need infer package to conduct t tests.
Let’s use our Console pane (NOT this Quarto document) and load infer package by using install.packages() function.

install.packages("infer")

Introduction - III

After loading that package, let’s use library function and load the data sets that we will use today.

library(tidyverse)
library(infer)
library(palmerpenguins)
data("penguins")

Example of a Case:

Imagine that you are a biologist studying penguins, particularly their bill lengths. You hypothesize that the average bill length of penguins is 40 mm and you collect a random sample of 344 penguins, measure and record their bill length in mm.

Perform a one sample \(t\)-test to investigate whether the bill length of the penguins differs from the test value of 40 mm. Use the 5% significance level (\(\alpha = 0.05\)).

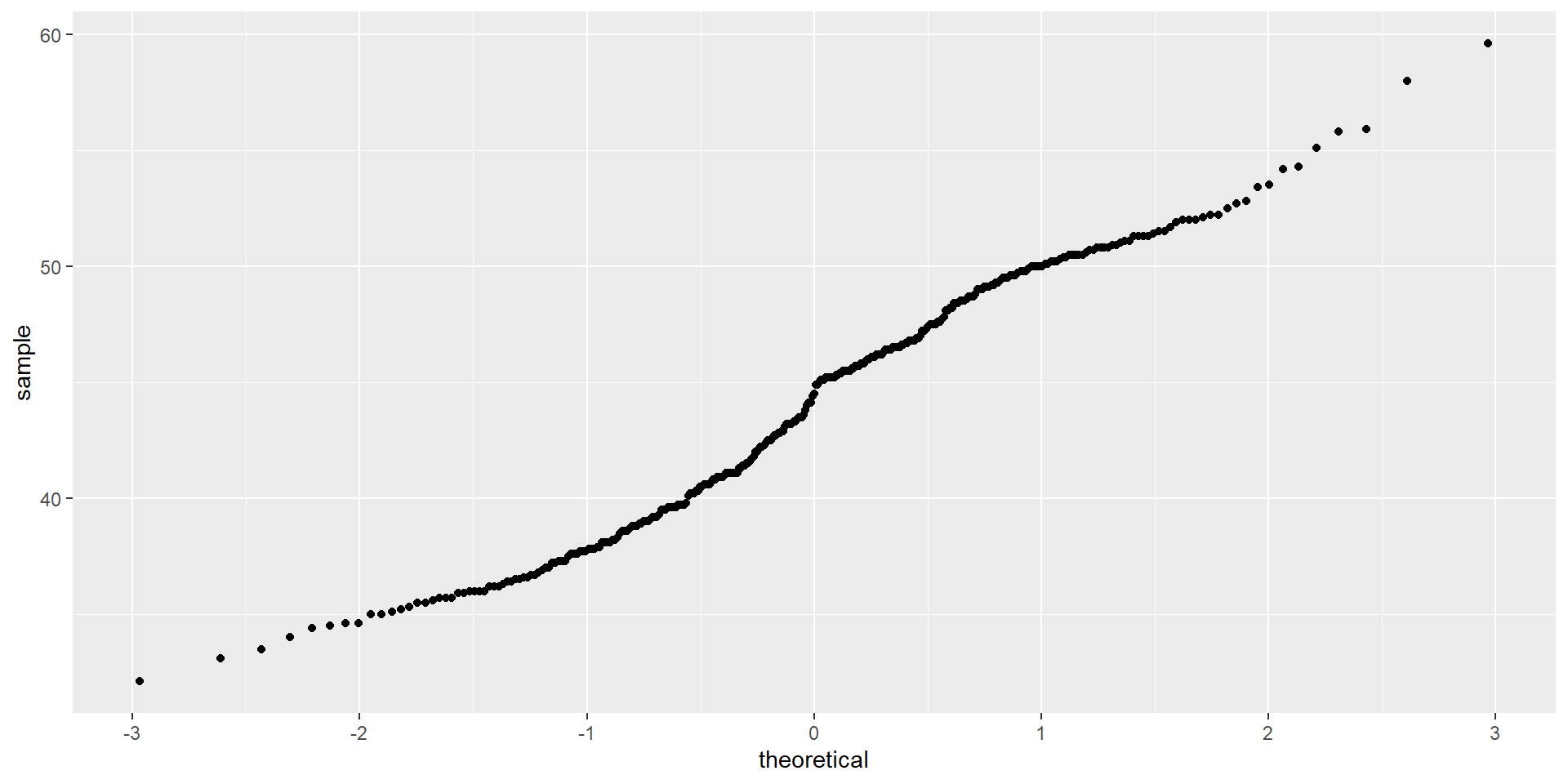
Checking the Normality Assumption

Check your sample size first!
- \(n\) > 50, so we can check visual plots.

Quantile Plot

ggplot(data = na.omit(penguins),
       aes(sample = bill_length_mm)) +
  geom_qq()

Interpreting the Output

t_test(penguins, response = bill_length_mm, mu = 40)

# A tibble: 1 × 7
  statistic  t_df  p_value alternative estimate lower_ci upper_ci
      <dbl> <dbl>    <dbl> <chr>          <dbl>    <dbl>    <dbl>
1      13.3   341 9.58e-33 two.sided       43.9     43.3     44.5

Conclusion: As \(P\)-value is very small, we can reject \(H_0\) and conclude that our data provided sufficient evidence to support the claim that the bill length of the penguins differs from 40 mm.

Confidence Interval: Type your confidence interval statement to your worksheet!

Independent Samples \(t\)-test

Example of a Case:

Now, you’re curious about the difference in the body mass of penguins based on their sex. You hypothesize that body mass varies between different sexes. To test your hypothesis, you collect a random sample of 344 penguins, measure their body mass, and record their sex.

Perform an independent samples \(t\)-test to investigate whether the body mass of penguins differs between different sexes. Use the 10% significance level (\(\alpha = 0.10\)).

Checking the Normality Assumption

Check your sample size first!
- \(n\) > 50, so we can check visual plots.

Quantile Plots

ggplot(data = na.omit(penguins),
       aes(sample = body_mass_g)) +
  geom_qq() +
  facet_wrap(~sex)

Interpreting the Output

t_test(x = penguins, 
       formula = body_mass_g ~ sex, 
       order = c("male", "female"),
       alternative = "two-sided",
       conf_level = 0.90)

# A tibble: 1 × 7
  statistic  t_df  p_value alternative estimate lower_ci upper_ci
      <dbl> <dbl>    <dbl> <chr>          <dbl>    <dbl>    <dbl>
1      8.55  324. 4.79e-16 two.sided       683.     552.     815.

Conclusion: Type your conclusion statement to your worksheet!

Confidence Interval: Type your confidence interval statement to your worksheet!